归并算法的过程

分而治之

归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案”修补”在一起，即分而治之)。

可以看到这种结构很像一棵完全二叉树，本文的归并排序我们采用递归去实现（也可采用迭代的方式去实现）。分阶段可以理解为就是递归拆分子序列的过程，递归深度为$log_2n$。

合并相邻有序子序列

再来看看治阶段，我们需要将两个已经有序的子序列合并成一个有序序列，比如上图中的最后一次合并，要将$[4,5,7,8]$和$[1,2,3,6]$两个已经有序的子序列，合并为最终序列$[1,2,3,4,5,6,7,8]$，来看下实现步骤。

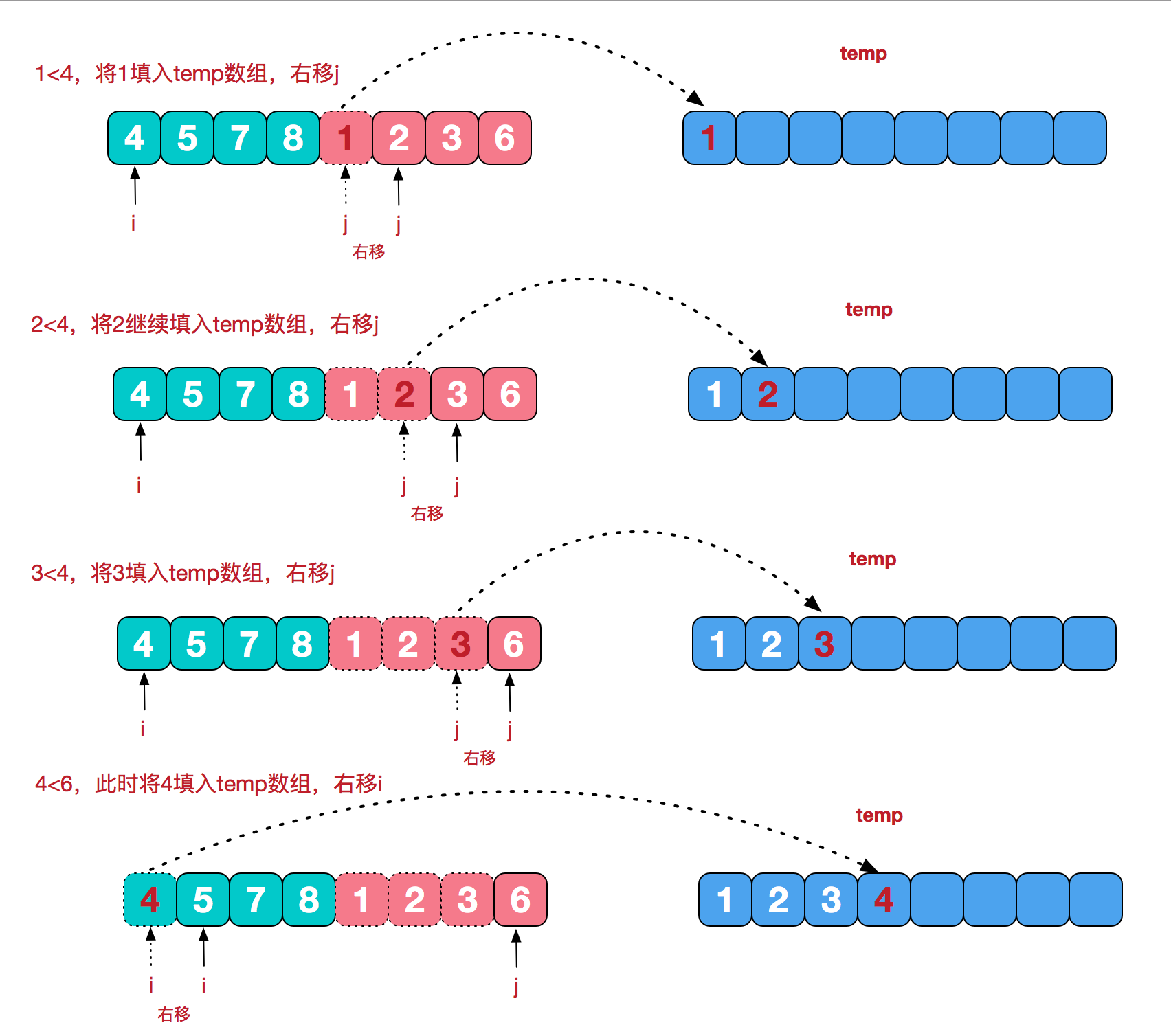
代码实现

Kotlin

package BaseAlgorithm

fun main(args: Array<String>) {
    sort(arrayOf(9, 18, 7, 36, 95, 24, 31, 72, 1))
}

/**
 * 归并排序
 *
 * @param array 代排序的数组
 * */
private fun sort(array: Array<Int>) {
    // 初始化一个大小为array.size的空数组
    val temp = Array(array.size, { 0 })
    println(array.toList())
    // 开始排序
    sort(array, 0, array.size - 1, temp)
    println(temp.toList())
}

/**
 * 归并排序——分离
 *
 * @param array 代排序的数组
 * @param left  左下标
 * @param right 右下标
 * @param temp  存放每次排序后的数组
 * */
private fun sort(array: Array<Int>, left: Int, right: Int, temp: Array<Int>) {
    if (left < right) {
        val mid = (left + right) / 2
        // 对左边的进行排序
        sort(array, left, mid, temp)
        // 对右边的进行排序
        sort(array, mid + 1, right, temp)
        // 对排序后的数组进行合并
        merge(array, left, mid, right, temp)
    }
}

/**
 * 归并排序——合并
 *
 * @param array 代排序的数组
 * @param left  左下标
 * @param mid   中间下标
 * @param right 右下标
 * @param temp  存放每次排序后的数组
 * */
private fun merge(array: Array<Int>, left: Int, mid: Int, right: Int, temp: Array<Int>) {
    var i = left
    // j默认从中间的右边地一个元素
    var j = mid + 1
    var t = 0

    // 将左边和右边的排序好的数组依次复制到temp数组中
    while (i <= mid && j <= right) {
        if (array[i] <= array[j]) temp[t++] = array[i++]
        else temp[t++] = array[j++]
    }

    // 将左边剩余的元素复制到temp数组中
    while (i <= mid) temp[t++] = array[i++]
    // 将右边剩余的元素复制到temp数组中
    while (j <= right) temp[t++] = array[j++]

    // 将数组从temp中复制到array
    t = 0
    i = left
    while (i <= right) array[i++] = temp[t++]
}

最后

归并排序是稳定排序，它也是一种十分高效的排序，能利用完全二叉树特性的排序一般性能都不会太差。Java中Arrays.sort()采用了一种名为TimSort的排序算法，就是归并排序的优化版本。从上文的图中可看出，每次合并操作的平均时间复杂度为$O(n)$，而完全二叉树的深度为$log_2n$。总的平均时间复杂度为$O(n \lg n)$。而且，归并排序的最好，最坏，平均时间复杂度均为$O(n \lg n)$。

作者： dreamcatcher-cx
出处： http://www.cnblogs.com/chengxiao/
本文版权归作者和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在页面明显位置给出原文链接。